latest transformを利用してdocumentの履歴を管理する
文書の変更履歴を追いたい場合、SQLでは「履歴テーブル」を利用することが多いかもしれません。
ここではウィンドウ関数「row_number」を使って工夫していますが、毎クエリで論理ドキュメントIDごとにaggregationして最新ドキュメントを取ってくるのも大変です。
elasticsearchでは同様の文書履歴の管理はできるでしょうか。「elasticsearch document history」などで検索するとちょっと古い質問がヒットします。
Elasticsearch - Maintaining Document History - Stack Overflow How to store document history (versioning, revisions)? - Elasticsearch - Discuss the Elastic Stack
「できません」という回答が目に留まります。
一方で、elasticsearchの7.11(2021/2)からData Transformに「latest」が追加され、利用できるようになりました。
(Data Transform機能については↓こちらが分かりやすいです。「OSS版のElasticsearchでは使えない」とあるが、今はFREE AND OPENでも利用可能っぽい?)
このlatest機能によって、"履歴インデックス"から論理IDごとに最新の文書を取得し、宛先のインデックスに自動で投入できるようになります。
body = {
'source': {'index': 'test_source'},
'latest':{'sort':'更新日時フィールド',
'unique_key': '論理IDフィールド'}
}
以上の内容のtransformを登録すれば、transformが定期的に(defaultでは1分ごと)実行され、論理IDごとに最新の文書のみを保持したインデックスが生成されます。
ノード障害時には回復プロセスが一部のTransformationを繰り返す可能性はありますが、データのconsistencyは保たれるようです(How transform checkpoints work / Error handling)。
一方で、ソースインデックスは必要に応じて論理IDおよび更新日時以外のフィールドを ・{'type': 'object', 'enabled':False} ・{'type': varies, 'index: false, 'doc_values': false} などとすることでインデックスサイズを節約することもできそうです。
{'type': 'object', 'enabled':False}としてしまうと、データのチェックが効かないので基本的には後者が良いでしょうか。
また、latestおよびunique_keyで指定するフィールドは、doc_value: Trueとする必要がありました。indexはFalseにしてもData Transformは実行されましたが、performance上の問題が生じ得るのでTrueにしておいた方が無難かもしれません。
参考までに。
VideoContainerChangerがエラーになるのでMTSをMP4に変換するバッチファイルを作成した
VideoContainerChangerというソフトがあり便利に使っていたのだが、久しぶりに使ってみようとダウンロードしてきたらうまく動かなかった。同梱されていたv1.1もv1.3もファイルを変換するとエラー。ffmpegを最新にしてもダメ。
以下のようなエラーがでてしまう。
ffmpeg version N-104423-g682bafdb12-20211024 Copyright (c) 2000-2021 the FFmpeg developers
built with gcc 10-win32 (GCC) 20210408
configuration: --prefix=/ffbuild/prefix --pkg-config-flags=--static --pkg-config=pkg-config --cross-prefix=x86_64-w64-mingw32- --arch=x86_64 --target-os=mingw32 --enable-gpl --enable-version3 --disable-debug --disable-w32threads --enable-pthreads --enable-iconv --enable-libxml2 --enable-zlib --enable-libfreetype --enable-libfribidi --enable-gmp --enable-lzma --enable-fontconfig --enable-libvorbis --enable-opencl --enable-libvmaf --enable-vulkan --disable-libxcb --disable-xlib --enable-amf --enable-libaom --enable-avisynth --enable-libdav1d --enable-libdavs2 --disable-libfdk-aac --enable-ffnvcodec --enable-cuda-llvm --enable-frei0r --enable-libglslang --enable-libgme --enable-libass --enable-libbluray --enable-libmp3lame --enable-libopus --enable-libtheora --enable-libvpx --enable-libwebp --enable-lv2 --enable-libmfx --enable-libopencore-amrnb --enable-libopencore-amrwb --enable-libopenjpeg --enable-librav1e --enable-librubberband --enable-schannel --enable-sdl2 --enable-libsoxr --enable-libsrt --enable-libsvtav1 --enable-libtwolame --enable-libuavs3d --disable-libdrm --disable-vaapi --enable-libvidstab --enable-libx264 --enable-libx265 --enable-libxavs2 --enable-libxvid --enable-libzimg --enable-libzvbi --extra-cflags=-DLIBTWOLAME_STATIC --extra-cxxflags= --extra-ldflags=-pthread --extra-ldexeflags= --extra-libs=-lgomp --extra-version=20211024
libavutil 57. 7.100 / 57. 7.100
libavcodec 59. 12.100 / 59. 12.100
libavformat 59. 8.100 / 59. 8.100
libavdevice 59. 0.101 / 59. 0.101
libavfilter 8. 15.100 / 8. 15.100
libswscale 6. 1.100 / 6. 1.100
libswresample 4. 0.100 / 4. 0.100
libpostproc 56. 0.100 / 56. 0.100
Input #0, mpegts, from 'C:/xxxx.MTS':
Duration: 00:05:38.85, start: 1.033367, bitrate: 16626 kb/s
Program 1
Stream #0:0[0x1011]: Video: h264 (High) (HDMV / 0x564D4448), yuv420p(top first), 1920x1080 [SAR 1:1 DAR 16:9], 29.97 fps, 59.94 tbr, 90k tbn
Stream #0:1[0x1100]: Audio: ac3 (AC-3 / 0x332D4341), 48000 Hz, 5.1(side), fltp, 448 kb/s
Stream #0:2[0x1200]: Subtitle: hdmv_pgs_subtitle ([144][0][0][0] / 0x0090), 1920x1080
[mp4 @ 000001c7aee4ca00] track 1: codec frame size is not set
[mp4 @ 000001c7aee4ca00] Could not find tag for codec hdmv_pgs_subtitle in stream #2, codec not currently supported in container
Could not write header for output file #0 (incorrect codec parameters ?): Invalid argument
Error initializing output stream 0:2 --
Stream mapping:
Stream #0:0 -> #0:0 (copy)
Stream #0:1 -> #0:1 (copy)
Stream #0:2 -> #0:2 (copy)
Last message repeated 1 times
Windowsのフォトを使う方法も簡便で良いが、再エンコードがかかっていそう。そこでffmpegを直接利用するバッチファイルを作成したのでメモしておく。
ffmpegをダウンロードしてきたら、ffmpeg.exeと同じフォルダに以下の内容のバッチファイルを置いて、動画をドラッグアンドドロップするとMP4ファイルに変換される。複数まとめてドラッグアンドドロップしても大丈夫。パスやファイル名に空白があっても大丈夫なはず。出力と同じ名前のファイルがある場合は確認される。
for %%f in (%*) do ( %~dp0\ffmpeg.exe -i "%%~f" -codec:v copy -codec:a copy "%%~dpnf_REMUX.mp4" ) pause
ffmpegと違う場所に置きたい場合は「%~dp0\ffmpeg.exe」の部分をffmpegのパスに変更する。ffmpegにパスを通してるなら「ffmpeg」でok。
出力ファイルを変更したければ、「"%%~dpnf_REMUX.mp4"」の「_REMUX.mp4」の部分を変更する。ffmpegは出力ファイルの拡張子で形式を判断しているので拡張子は変更しない方が良い。
「-codec:v copy」と「-codec:a copy」はそれぞれ、動画と音声はコーデックを変換せずに元の形式をコピーするという意味。これで再エンコードせず、containerのみの変換になる。
処理結果が見れた方がうれしいので最後に「pause」を入れているが、終了して欲しい場合は省く。
手元のMTSファイルしか試してないけども、コンテナ変換なので.m2tsとか.tsも行けるはず。
参考: Video Container Changerv1.1 はWin10で使える方法あるのでしょうか -T- 画像編集・動画編集・音楽編集 | 教えて!goo
「交絡因子で調整した」とはどういうことか
重回帰分析において、交絡因子を調整するためには、モデルに交絡因子を投入すればよい、とよく言われます。 なんとなくそういうものかと思ってきましたが、その意味を少し考えてみました。今回は2つの項のみの単純化したモデルですが、より複雑なモデルについても同様の考え方ができるはずです。交絡因子と、暴露/治療と相関する部分についてはどちらの係数に寄与するのか理解していませんでしたが、乱暴な言い方をすれば重回帰モデルにおいては「アウトカムとの相関の程度に応じて割り振られる」と考えることができそうです。
例は適当に考えたので、DAGの妥当性については目をつぶってください。
スライドをそのまま貼り付けています。





参考: 重回帰分析をN次元空間で考える、ということについてはこのページの下半分が分かりやすかった。 www.snap-tck.com
BART: Bayesian additive regression treesによる因果推論
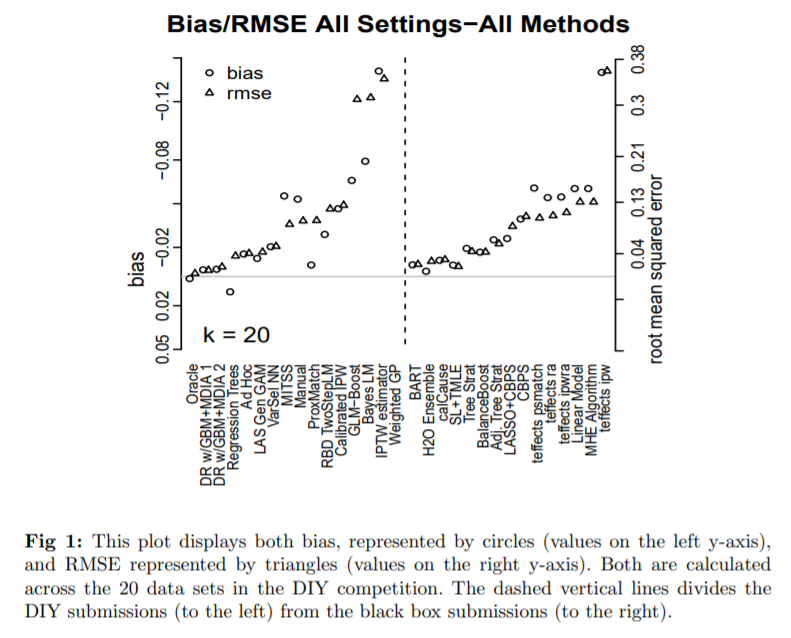
Atlantic Causal Inference Conference 2016の結果をまとめた論文.
このコンペはstrong ignorabilityを仮定したシチュエーションにおいて,線形・非線形の77種のdata generating process (DGP)を仮定し,各々のDGPについて100回ずつn=250 or 500のdatasetを生成した計7700個のデータセットで因果推論を行うコンペ.20個のデータセットが提示されて試行錯誤できるdo-it-yourselfセクションと,手法を提出して7700個のデータセット上で評価されるblack-boxセクションから構成されている.
個人因果効果を算出するモデルの中ではBARTというモデルを活用したものが一番成績がよかった模様.あまり聞いたことのない手法だったので,ざっと調べてみた.以下、年代順に重要そうな論文を3つ紹介する。
BART: BAYESIAN ADDITIVE REGRESSION TREES
[0806.3286] BART: Bayesian additive regression trees
BART自体は最新の予測モデルというわけではなく,Chipman 2007, 2010などで提案された予測モデル.具体的にはリンクの論文や,次のセクションで紹介するHill, 2010の§3.1に詳しいが,理解した範囲で概要を紹介する.
まず,m個(元論文では200個)の木による加法的予測モデル(以下1個の予測モデルを森と呼ぶ)
を考え,これをベイズで求めることを考える.初期値は適当なpriorからサンプリングして森を作成したのちに,木を1個ずつMCMCで更新していく作業を繰り返していく.各更新では尤度比に応じて棄却するか更新するか決定される.これが収束したところで事後分布に応じたK個の森をサンプリングし,予測する際はK個の森を使うことで予測値の事後分布を得るというモデル.これ自体は予測モデルであり,因果推論のためのモデルというわけではない.
残差を予測するような木を加法的に用いる点はGBDTに似ているが,ひたすら足していくのではなく一定の数の木を周回して更新していくところと,過学習を防ぐ手段として正則化項を加えるのではなくpriorによって複雑さを抑制しているところが大きな違いか.
メリットとしては事後分布をを得られるということ.当然,点推定値だけではなく区間推定どころか分布で結果が得られる.事後分布が妥当な広がりを持っているかは,問題に応じた複雑さと,priorが規定する複雑さが合致するかどうかに依存すると思うのだけど,経験的にこのぐらいのpriorがよかったよというのが本文中で紹介されていて,一部のパラメータについてはデフォルトでも良いがcross-validationで決めてもよいとされている.
BARTによる因果推論
Bayesian Nonparametric Modeling for Causal Inference Jennifer L. Hill

3.1がBARTの概論.3.2からBARTによる因果推論.基本的には因果推論として特別なことをするわけではなく,treatmentも他のcovariateと同列に扱った予測モデルを構築し,その上でtreatment Z={0,1}とした予測値の差で因果効果を推定するアプローチ.K個の森を得られているので,因果効果の事後分布に沿ったK個の推定値を得ることができいる.よって上の図のように,その95%信用区間を算出できる.
An overall benefit is the lack of “tinkering” required with BART. Researchers tend to condition on variables and use functional forms that fit their existing theory (for a discus- sion, seeLeamer 1983). Moreover, when searching for the “best” model it may be difficult not to stop as soon as the model meets prior expectations or to bypass models that do not meet prior expectations. Such model-searching strategies, while understandable, particu- larly given strong theory regarding a phenomenon, have the potential to mask important but unexpected results and bias estimates.
authorのHillは,事前の知識や因果構造についての推論などをモデル化に活用すると,予測していなかった重要な結果をマスクしてしまったり,推定にバイアスを生んでしまう,という立場を取っている.なので事前知識に応じた既知の因果構造を取り込んだpriorを設定するといった方法論の記載は論文内にない.
BART on PScore
ACIC2016においてBARTが,(random forest, GBDT, neural networkなどによる)ensembleモデルに匹敵する唯一の手法だったことから,コンペ終了後にBARTをベースとしたいくつかの手法が試された.BART on PScore(typoじゃないよ)は,別で推測したpropensity scoreをcovariateとしてBARTによる予測モデルの入力に加えた手法らしい.以下の論文からinspireされた方法とのことで確かに4章がほぼほぼその説明になっている。
この論文の前半4章までが上記のBART on PScoreの説明である。ここで問題視されているのは、vanilla BARTにおいてPrognosis→propensity scoreに単調な関係があるようなとき(これは、治療しないと重症になる人ほど治療を受けやすいということで非常によくある関係である)、priorにかなり影響されてしまうregularization-induced confoundingという性質。
nonlinear modelにおける解説は難しくてよくわからないので、単純な線形モデルで示してあった例(p10)を載せておく。
が成立しているとき、bを任意のバイアスパラメータとして、
が常に成立する。もしが
よりも高い事前分布が割り当てられているとき、
が、Yの分散
よりも十分に小さければ、
の推定は、
に向かってバイアスが生じる。
これはZ|xの分散が小さい、つまり治療がxによってほぼほぼ決まっているような状況でZの影響とxの影響を識別できず、知りたい因果効果であるの事後分布がpriorの分布に依存してしまうということ。(これはcommon supportが少なくてうまくマッチングしないとか、propensity scoreが1or0に近づいてしまってIPW推定が不安定になるといった状況にも近いと思うのだけど、そこでpriorへの依存性が高まるというのがベイズらしくて面白い)。
では、このpriorへの依存をどうすればよいのかという話が4.3節にある。Yを予測するときにXとZの効果を分離したいのに、例えば極端なケースで、のように
が
の関数になっている場合など、
に伴う
の変動を
の影響と捉えてしまうかもしれない。ここから先は実はよくある話で、その解決策は
を共変量に加えることである。もちろん
は推定しなければいけないのだが、これはcouterfactualもなく単にpredictionの問題なので回帰問題として解けば良い。
で条件付けられたもとでは、
と
は独立になるので、前項で挙げたような任意のバイアスパラメータで等式が成立することもなく、biasへの依存性の問題は緩和される(らしい)。
Bayesian causal forest
5節以降で、新たなモデルとしてbayesian causal forestというモデルが紹介される。strong confounding, targeted selection, and relatively weak treatment effectsがあるような状況で特に有用とのこと.
vanilla BARTやBART on PScoreでは,割付zは他の共変量と同格に共変量として予測モデルに組み込まれているのみであり,治療効果はいわば間接的にz=1を入力した時の予測値とz=0を入力した時の差として推測されていた.このようにモデル化すると、Yの分散に対して因果効果が相対的に小さい時(そしてそれは因果効果推論においてよくある状況である)、推定因果効果の分散がYの分散以上に大きくなって有意義な推論ができなくなってしまう。よって、治療効果をより直接推測するために下記の変更をおこなった(前節の考察を生かして、prognostic modelにが加えられている)。
とも独立したpriorからBARTのアルゴリズムよって求められる.なお,ここで
はpropensity scoreの推定値である.
についてはChipmanのデフォルトのパラメータと同じものを使うことをを推奨しているが、
についてはより制限されたpriorが推奨されている。これは、treatment effect heterogeneietyのパターンが、Y|xのパターンよりも単純だと想定しているため。よって木の数はより少なく、また木の分岐も減るようなpriorの設定となっている。また、事前分布の中央値はYのSDに一致するように設定するとのこと。
このモデルをACIC 2016のdatasetに対して使用した場合の結果がTable2, 3.に掲載されている。
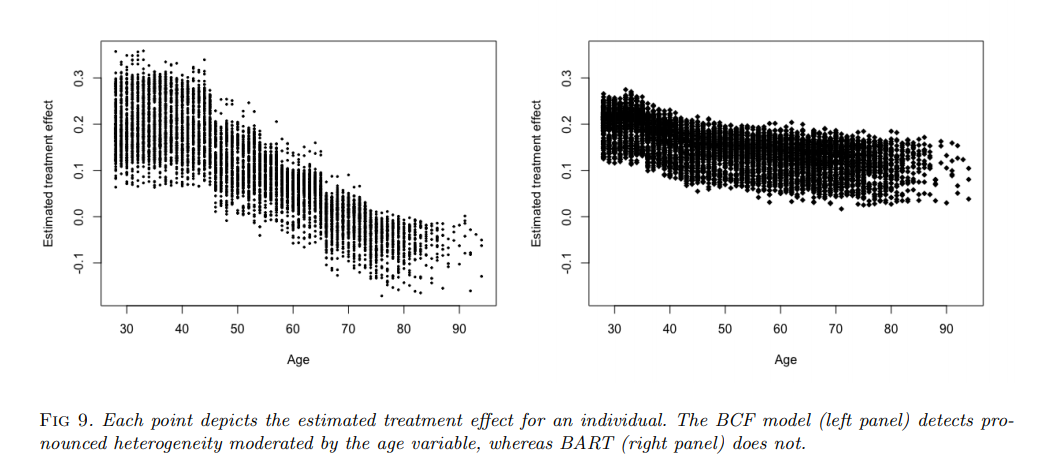
また、喫煙による医療支出への影響を調べた実データにも適用しており、vanilla BARTとの特性の違いが示されている。シミュレーションデータではないので真のデータは分からないのだが、年齢によるcausal effect heterogeneityをうまく捉えているように見える。
感想
最後のbayesian causal forestは、今までの手法の課題を解決する納得感のあるモデル。causal effect自体をモデルにするという部分はX-learnerの目的意識に近いと感じるが、ベイズの柔軟性を生かしてさらに直感的なモデリングとなっている印象。causal effectのpriorを調整することでsensitivity analysisを行うこともできそう。
Rのライブラリも公開されており、ぜひ使ってみたい。 bcf: Fit Bayesian Causal Forests in bcf: Causal Inference for a Binary Treatment and Continuous Outcome using Bayesian Causal Forests
Hernán MA, Robins JM (2020). Causal Inference: What If.のPart IIをざっくりとまとめる①
Hernan先生のCausal Inferenceを読み進めています.英語で読んでいくとなかなか全体像がつかみづらかったりするので,適宜まとめながら読んでいました.Part IIについては全体の流れは概ね理解できた気がするのでせっかくなので記事にしておきます.Oct 26の版に準拠して該当するページや章を記載していますが,今後の改訂によって多少ずれるかもしれません.
Part Iは無限のpopulationを仮定した理想的な状況での因果推論の定性的な議論です.Part IIは実問題に応用できるようどのようにモデル化して解析するかの手法が紹介されており,Part IIIは時間依存性介入や時間依存性交絡についてのSectionという3部構成になっています.
Part Iのcausal graph(DAG)やconfounding,counterfactual outcomeなどの説明は割愛します.
Notation
$A$: treatment
$L$: confounders
$Y$: outcome
$Y^{a}$: conterfactual outcome
TP: Technical Point
FP: Fine Point
この本の因果推論における前提 (Ch13.5)
- identifiability conditions: exchangeability, positivity, consistency (Chapter 3)
- all variables are correctly measured. (Chapter 9 measurement error)
- all models are correctly specified (Chapter 11). model misspecification.
これらの条件を確認するのが,ingestigator's most important taskであるとのこと.この本で説明されている手法の多くは上記の条件を前提としています.
また,本文中にはrandomでないcensoringに対応する手法も記載がありますがconfoundingへの対処と本質的にあまり差がない気がするのでこの記事では省略します.
conditional exchangeabilityを仮定する推定方法
因果推論における最大の関心領域であり,この仮定を前提とした手法が多いです.これは$Y^{a} ⊥ A|L$という条件であり,$L$が一致している人々の中では実際に治療された群も治療されなかった群も潜在的なアウトカムが等しいということです.この条件のもとでは$E[Y|A,L] = E[Y^{a}|L]$が成立するので,$L$が等しい人々のなかでは単純に治療群と非治療群のアウトカムを比較すれば$association=causation$となって交絡なく治療効果を推定することができます.実際には,$E[Y|A,L] = E[Y^{a}|L]$はmean exchangeabilityと呼ばれ,独立ではなくてもこちらさえ成立していれば以下に扱うようなaverage causal effectの推論には十分なようです(Technical Point 2.1参照).
なお,Part IのCh.8あたりに詳しく説明されていますが,$A→Y$の因果効果推定に際して調整すべき交絡因子(confounding factors)は一意に定まるわけではありません.例えば,$A←L1→L2→Y$というcausal graphを考慮したとき$L={L1}$も,$L={L2}$も,$L={L1, L2}$もいずれであっても,調整することで十分に交絡に対処できます(Ch.8).
この本では事前知識などにより構築したcausal graphのもとで調整すべき$L$を検討するという立場を取っており,データからcausal graphを構築する因果探索的なアプローチはこの本のscope外です.以下に,conditional exchangeabilityを仮定する推定方法を挙げていきます.本文ではsubgroup上のATEや,ある共変量によるeffect modificationを推定する方法も登場しますが,この記事ではまずaverage causal effect (ATE)を推定する方法を取り上げます.
Nonparametric estimators of the conditional mean(Ch.11.3)
まずひとつ目はこれ.Part Iでも取り上げられました.すべての$A$と$L$が離散的で、かつサンプル数が無数にある(というやや非現実的な)とき、すべての$A, L$の組み合わせに対して十分なサンプルがあるのでその各セルに対してconditional mean: $E[Y|A, L]$を直接計算することで$E[Y^{a}|L]$が求められます.そして後で取り上げるstratification(=g-formula)の考え方を使って,全サンプルの$L=l$に対して$E[Y|A=a, L=l]$を計算して平均を取ることでaverage causal effect (ATE)を推定することができます.
モデル化の必要性
しかしA, Lに連続量を含む場合やLが高次元な場合など,$E[Y|A, L]$を$A, L$の組み合わせごとに求めていてはうまく計算できないことが多く,何らかのモデルを仮定してsmoothingする必要があります(言い換えると,Lが少し違うサンプルの情報を借りてきて,$E[Y^{a}|A,L]$を推定しなければいけない).
モデル化の方法としては,この本での主題となるg-methodsとstratification-based methodsに大きく2つに分けることができます(p95).以下,一つずつ見ていきます.
g-methods
g-methods①: IP weighting
IPWによるpseudo-population上で$E[Y|A] = \theta_0 + \theta_1A$を回帰することで,marginal structural mean model: $E[Ya] = \beta_0 + \beta_1a$を推定します.marginal structural mean modelは個々のサンプルについてのYの回帰式ではなく,Yの平均構造についての回帰式だと思います.p157に,もし知りたいパラメータが母集団全体のATEであれば,marginal strucural mean modelは共変量の項を含まないとあります.(なおmarginal structural mean modelはAが2値であればAについてはsatured modelであり,本質的にはmodelではなくsmoothingの効果はない.Aがcontinuousな場合は何らかのsmoothingがなされる).
Aについてsaturedなmodelでは関係ありませんが,Aについてもモデル化するような場合は,stabilized IP weighingと言って,$\frac{1}{\pi[a|l]}$のかわりに$\frac{f(A=a)}{\pi[a|l]}$を用いた方がvalidな推定ができると書かれていました(Ch.12.3).
IP weighing法におけるモデル化の核は,$E[A|L] =\pi (L)$のモデル化であり,logistic regressionなどが用いられることが多いです.Propensity scoreを用いる手法全てに共通することですが,$L$にoutcomeには弱く影響しtreatmentに強く影響するような(言ってしまうと操作変数に近いような)変数を含んでいると推定が不安定になることが欠点です.
また,$A$がcontinuousな場合は$\pi(L)$は何らかの確率密度分布probability density function (pdf)を出力する必要があり,かつこの誤設定に敏感なのでかなり慎重にならなければならないと述べられています.
(p.156) Unfortunately, pdfs are generally hard to estimate correctly, which is why using IP weighting for continuous treatments will often be dangerous. One should be careful when using IP weighting for continuous treatments because the effect estimates may be exquisitely sensitive to the choice of the model for the conditional density f(A|L).
IPW自体はたくさんのblogでも紹介されているので深入りしませんが,一応TP3.1の式変形を追っておきます.
$$ \begin{eqnarray} E[Y^{a}] &=& \sum_{l}E[Y^{a}|L=l]Pr[L=l]\\ &=&\sum_{l} {E[Y|A=a, L=l] Pr[L=l]}\\ &=&\sum_{l} \frac{1}{\pi [a|l]}{E[Y|A=a, L=l] \pi[a|l]Pr[L=l]}\\ &=&\sum_{l} \frac{1}{\pi [a|l]} I(A=a)Y Pr[L=l]\\ &=& E\left[\frac{I(A=a)Y}{\pi[a|l]}\right]\\ &=& \frac{\sum \frac{I(A=a)Y}{\pi[a|l]}} {\sum \frac{1}{\pi[a|l]}} \end{eqnarray} $$
$E[Y|A=a, L=l] \pi[a|l] = I(A=a)Y$の部分の変形がややトリッキーですが,$A=a$の時の期待値に$A=a$となる割合をかけているので,この部分は,
$$ I(A=a)Y = \left\{ \begin{array}{} Y & (A=a)\\ 0 & (A\neq a) \end{array} \right. $$ の期待値に等しくなります.また,最後は${\sum \frac{1}{\pi[a|l]}}$がtotal populationのNに等しくなるためです.
g-methods②: standardization and the parametric g-formula (Ch.13)
こちらはIPWより見かける機会は少ないかもしれません. $$ ATE = \sum_{l} E[Y|A=a, L=l] Pr[L=l] $$ IP weighingではサンプル毎に重みをかけてconterfactualを推定しましたが,L=lの層ごとに考えて層の重みでsummationしています.summationはLでの期待値とみなせるので,L=lの層内でYの期待値(conditional mean outcome)を取った後にLについて期待値を取ったdouble expectationと解釈できます.
実はIP weightingの式変形の途中で同じ式が出現しており,結局は同じものを求めていますが,モデル化する部分が違うのです.
上式のconditional mean outcomeにそのestimateを代入(plug-in)したものを,plug-in g-formulaと呼びます.例えば,$\hat{E}[Y|A=a, L=l]$として,$A, L$を変数としたoutcome regression model(例:$A$,$L$の一次項,二次項,一次の交互作用項などを入れた線形モデル)を考えることができます.
なお,$Pr[L=l]$は実際には推定する必要はなく,サンプルの全ての$l$について$\hat{E}[Y|A=a, L=l]$を計算して平均すればATEを求めることができます(empirical distribution).
また,後のstratification and outcome regressionでも,outcome regression model: $E[Y|A, L]$が出てきます.standardization (g-formula)のポイントは,$Pr[L=l]$をかけて和を取ることで母集団全体についての平均(=期待値)を取っているという部分だと思います.
g-methods③: doubly robust estimators(TP13.2)
doubly robust estimatorにもいろいろあるようで,FP13.2とTP13.2で少し違うモデルが取り上げられていますが,ここではTP13.2のものを載せておきます.
$$ \pi(L) = Pr[A=1|L=l]\\ b(L) = E[Y|A=1,L] = E[\frac{AY}{\pi(L)}] $$
として,それぞれの推定式を$\hat{\pi}(L)$,$\hat{b}(L)$と表します.ここで,doubly robust estimatorは,
 となります(Texclipではうまく表示できるがhatenaだとうまく表示できず...).
となります(Texclipではうまく表示できるがhatenaだとうまく表示できず...).
証明は追えていないのですが,この時のbiasはIPWのerror$\frac{1}{\pi(l)}-\frac{1}{\hat{\pi}(l)}$と,outcome modelのerror$b(l)-\hat{b}(l)$との積になるため,doubly robustと呼ばれます.
g-methods④: structural nested models and g-estimation (Ch.14)
これも星野本などではあまり取り上げられていない手法だと思います.ただ,時間依存性介入のような複雑な状況でなければover killであるとも述べられており,Part IIIへの準備という側面が強いのかもしれません.p180には"In fact, structural nested models of any type have rarely been used"とあります.
これはconditional exchangeabilityを逆手に取ったような手法です.conditional exchangeabilityのもとでは$A$と$Y^{a}$は独立であり,Lに加えて$Y^{a}$を条件づけたところでA=aの分布は変わらない,つまり, $$ Pr[A=1|Y^{a=0},L]=Pr[A=1|L] $$ が成り立っているはずで, $$ logit Pr[A=1|Y^{a=0},L] = \alpha_{0} + \alpha_{1}Y^{a=0}+\alpha_{2}L $$ を推定すると$\alpha_{1}=0$になるはずだ,というロジックです.そこで$Y^{a=0}$の候補を虱潰しにサーチして,$ \alpha_{1}$が0になればそれが正しい$Y^{a=0}$だろうというわけです.
かといって任意の$Y^{a=0}$を調べることは計算量が爆発しますし,解も無限に出てきてしまいそうです.そこで,causal effectの式を少し変形してstructural model: $$ E[Y^{a}-Y^{a=0}|A=a,L]=\beta_{1}a $$ を考えます.このmodelはstructural nested mean modelとも呼ばるそうですが,"nested"はtime-varying treatmentでのみnestedらしいのであまり気にしないでよさそうです(p173).
仮想的な$Y^{a=0}$として, $$ H(\psi^{\dagger}) = Y -\psi^{\dagger}A $$ を考えます.$\beta_{1}$としてありえそうな値の範囲として,(例えば教科書の例では)-20から+20まで0.01刻みで計算しています.その値を$\psi^{\dagger}$に代入した$H(\psi^{\dagger})$を使ってlogistic regressionまで解き,$ \alpha_{1}=0$にもっとも近い結果が得られる$\psi^{\dagger}$が,$\beta_{1}$の不偏推定になるということのようです.
なお,ここでは単一パラメータのモデルのみ取り上げましたが,複数のパラメータを持つモデルでは制約が一つだと複数の候補がでてきてしまいます.そこでパラメータ数と同じだけの制約を設けるために,$E[Y^{a}-Y^{a=0}|A=a,L]=\beta_{1}a + \beta_{2}aL$であれば,$logit Pr[A=1|Y^{a=0},L] = \alpha_{0} + \alpha_{1}Y^{a=0}+\alpha_{1}Y^{a=0}L + \alpha_{3}L$など項が対応したlogstic modelを考えてあげると良いです.
また,パラメータが増えると計算量がexponentialに増えてしまいますが,実際にはしらみつぶしに計算せずにclosed formで解くことができるそうなので,気になる方はTechnical Point(14.2)を見てみてください(よく分かりませんでした...).
長くなってきたので分けます.stratification-based methodsは次の記事で.
PubMedから医療AI論文を抽出してSlackに投稿する

元ネタ
一部slackのAPI仕様が変わってこともあり、微修正した。
Google Apps Script+Slack Appsで完結するようになった.
1. Pubmedの検索クエリを反映したRSSを作成する
 適当な単語で検索した後に,検索窓の下に出現する"Create RSS"からRSSのURLが得られる.
Core Clinical Journalでフィルタリングしようと思ったが,RSSにはフィルターは効かなかった.そもそもCore Clinical Journalは雑誌をカスタマイズできないので,最初から自分で作ったほうが良さそう.
適当な単語で検索した後に,検索窓の下に出現する"Create RSS"からRSSのURLが得られる.
Core Clinical Journalでフィルタリングしようと思ったが,RSSにはフィルターは効かなかった.そもそもCore Clinical Journalは雑誌をカスタマイズできないので,最初から自分で作ったほうが良さそう.
下記を参考に,各分野で上から1-2個の雑誌をor検索に入れた条件式を作成した.advanced searchに行くとGUIで作成できる.
Impact factorで分野の違いが考慮されていないわけがなかろうが(笑)[第二版] | 水道研究者の生態
((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((("The New England journal of medicine"[Journal]) OR "Lancet (London, England)"[Journal]) OR "JAMA"[Journal]) OR "BMJ (Clinical research ed.)"[Journal]) OR "Annals of internal medicine"[Journal]) OR "Journal of clinical oncology : official journal of the American Society of Clinical Oncology"[Journal]) OR "The Lancet. Oncology"[Journal]) OR "Nature medicine"[Journal]) OR "Circulation"[Journal]) OR "Blood"[Journal]) OR "European heart journal"[Journal]) OR "Gastroenterology"[Journal]) OR "Nature neuroscience"[Journal]) OR "Immunity"[Journal]) OR "British journal of anaesthesia"[Journal]) OR "Anesthesiology"[Journal]) OR "Clinical chemistry"[Journal]) OR "Clinical infectious diseases : an official publication of the Infectious Diseases Society of America"[Journal]) OR "Critical care medicine"[Journal]) OR "Critical care (London, England)"[Journal]) OR "The British journal of dermatology"[Journal]) OR "Diabetes care"[Journal]) OR "Diabetes"[Journal]) OR "Resuscitation"[Journal]) OR ("The Journal of clinical endocrinology and metabolism"[Journal])) OR ("MMWR. Morbidity and mortality weekly report"[Journal])) OR "International journal of epidemiology"[Journal]) OR "American journal of epidemiology"[Journal]) OR "Epidemiology (Cambridge, Mass.)"[Journal]) OR "Nature genetics"[Journal]) OR ("American journal of obstetrics and gynecology"[Journal])) OR "Leukemia"[Journal]) OR "Nature immunology"[Journal]) OR "Journal of medical Internet research"[Journal]) OR "Journal of the American Medical Informatics Association : JAMIA"[Journal]) OR "Journal of biomedical informatics"[Journal]) OR "International journal of medical informatics"[Journal]) OR "The Lancet. Neurology"[Journal]) OR "Neurology"[Journal]) OR "Brain : a journal of neurology"[Journal]) OR "Journal of neurosurgery"[Journal]) OR "Neurosurgery"[Journal]) OR "World neurosurgery"[Journal]) OR "The American journal of clinical nutrition"[Journal]) OR "Ophthalmology"[Journal]) OR "The American journal of sports medicine"[Journal]) OR "Pain"[Journal]) OR "Acta neuropathologica"[Journal]) OR "The Journal of pathology"[Journal]) OR "Pediatrics"[Journal]) OR "Biological psychiatry"[Journal]) OR "Psychological science"[Journal]) OR "Journal of general internal medicine"[Journal]) OR ("BMC pregnancy and childbirth"[Journal])) OR ("American journal of respiratory and critical care medicine"[Journal])) OR "American journal of public health"[Journal]) OR "Radiology"[Journal]) OR ("Fertility and sterility"[Journal])) OR ("Archives of physical medicine and rehabilitation"[Journal])) OR "Annals of the rheumatic diseases"[Journal]) OR ("Journal of personality and social psychology"[Journal])) OR "Annals of surgery"[Journal]) OR "Environmental health perspectives"[Journal]) OR ("American journal of transplantation : official journal of the American Society of Transplantation and the American Society of Transplant Surgeons"[Journal])) OR "PLoS neglected tropical diseases"[Journal]) OR "European urology"[Journal]) OR "Stroke"[Journal]) AND (((machine learning) OR deep learning) OR artificial intelligence)
参考までに作成した検索式を載せるが,かなり偏っているのでご自身で作成したほうが良いと思う.ちなみに"reinforcement learning"は,生物学的な強化学習そのものがたくさんヒットするので工夫のしどころ(とりあえず諦めた).

slackにはRSSリーダーもあるが,このRSSをそこに直接渡すと上記のようにまとめられてしまう.これはちょっと今ひとつ.
2. slack側の設定
旧tokenはもう推奨されないらしいので、下記の中ごろを参照してSlack Appsを作成した.

今回は通知するだけなので,Incoming Webhookのみ有効にすれば良い.Install Appsのところに,RESTに必要なURLが載っている.認証は必要なときに確認されるので画面に沿って進める.なお,投稿時のユーザー名はAppsで作成した標準のユーザー名が使用され,変更できなくなったらしい.
なお,APIの解説ページにslackのGUIアプリからはたどり着けなかったので,"api slack"などと検索してAPIのサイトに行くのが良いと思う.
3. Google Apps Scriptの作成
あとは元ネタの微修正.
変更点1
Incoming WebhookはPOSTで叩けるので,標準ライブラリのUrlFetchApp.fetchが使える.このため追加ライブラリのインストールが不要になった.(REST APIとJSONを使ったことがなかったで,この部分が地味に大変だった.blockのみをpayloadに入れていてうまく行かず1時間くらい溶かしたorz.1メッセージあたりの最大block数50の制約もトラップ.)
結局のところ,公式のdocumentが一番有用だったと思う.payload直下のtextは fallback string であり,メッセージがうまく読み込めなかったときやアラートなどに使用されるらしい.このtextを指定していないと,no_text errorが出続ける(出続けた).
Reference: Message payloads | Slack
変更点2
スプレッドシートを別で作るのがなんとなく嫌だったので,parameterを使って更新確認をしている.すべてテキストとして保存されてしまい,連番を管理するのがやや面倒だったので,','で区切って配列を実現している.GUIDの仕様が変わって上記の文字が含まれるようになると破綻するはず.
変更点3
英日翻訳したタイトルもつけた.
var title_ja = LanguageApp.translate(title 'en', 'ja')
これだけでテキストの翻訳ができる.至れりつくせり😊
変更点4
公開日も載せるようにした.CDATAセクションという,構造化されてないベタ打ち部分に入っているのがちょっと面倒.abstractも同様にして取得できるが,slackで眺めるには情報過多になりかねないので,タイトルから興味を持ったらリンクから飛ぶことで良しとした.
変更点5
deplecaitedが懸念されるAttatchmentではなく,Blockにした.これによってカスタマイズの幅が広がった.markdown記法に則ればいろいろ調整が効く模様.attatchmentではcolorを指定することで使えたブロックごとの左側の縦棒が使えない(これは公式でもattachmentからblockへ変更によってできなくなった唯一のことだと記載されている).
引用にすると色の指定はできないものの縦棒が出現して少し視認性が良いような気がするのでそうしてある.
慣れた人なら一瞬なのだろうけど,結構苦労したので最後にスクリプトを載せておく.Google Apps Scriptに貼り付けてHookURLとRSSのURLを変更すれば動くはず.
function PubMedSlack() { var HookURL = 'https://hooks.slack.com/services/xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx'; var N_IN_BLOCK = 5; var properties = PropertiesService.getScriptProperties(); var properties_dict = properties.getProperties(); // [keyword, RSS_URL]を要素に持つリスト。keywordはスクリプト内で一意にしてください。 var RSS_l = [['machine learning', 'https://eutils.ncbi.nlm.nih.gov/entrez/eutils/erss.cgi?rss_guid=xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx'], ['test', 'https://eutils.ncbi.nlm.nih.gov/entrez/eutils/erss.cgi?rss_guid=xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx']]; for (var i = 0; i < RSS_l.length; i++) { var keyword = RSS_l[i][0]; var feedURL = RSS_l[i][1]; var lastFetched = ['']; if (properties_dict[keyword]){ var lastFetched = properties_dict[keyword].split(','); }; //lastFetched = ['']//連続して試したいときはコメント解除を // Fetch try { var rssText = UrlFetchApp.fetch(feedURL).getContentText(); // たまにPubMedが404エラーを出すことがあるのでtryで回避 } catch (e) { continue; // もしエラーが出てもとりあえず無視(次回fetchできれば良しとする) } // Parse var rss = XmlService.parse(rssText); var items = rss.getRootElement().getChildren('channel')[0].getChildren('item'); // Check new items var news = []; for each(var item in items) { if (lastFetched.indexOf(item.getChild('guid').getText()) < 0) { news.push(item); } } if (news.length > 0) { // Prepare blocks var blocks = [{ type: "section", text: { type:"mrkdwn", text:'Here are ' + news.length + ' new papers for *"' + keyword + '"* :eyes:' } }]; var txt = ''; var j = 1; for each(var item in news) { var title = item.getChild('title').getText(); var title_ja = LanguageApp.translate(title,'en','ja'); var authors = item.getChild('author').getText().replace(/^\s+/, '').split(','); // なぜか先頭にあるスペースを削除 var author = authors[0]; if (authors.length>1){ author += ', _et al._'; }; var journal = item.getChild('category').getText() + '.'; var link = item.getChild('link').getText(); var description = item.getChild('description').getText(); var date = description.split('</p>')[1].split('. ')[1]; // var abstract = description.split('</p>')[3]; txt += '>*<'+link+'|'+title+'>*\n>'+title_ja+'\n>'+ author + ' ' + '_*' + journal + '*_ ' + date + '\n \n'; //5記事ごとに1block生成する //1記事ごとにブロックを生成するとブロック数の上限50にひっかかることがある //maximum length for the 'text' in a block is 3,000 characters. //messageあたりは100,000characters //1記事1メッセージしないのは無料版slackでメッセージ数を節約するため if ((j%N_IN_BLOCK)==0){ var l = txt.length; blocks.push({ type: "section", text: { type:"mrkdwn", text: txt } }); txt = ''; }; j += 1; }; if ((j%N_IN_BLOCK)!=1){ blocks.push({ type: "section", text: { type:"mrkdwn", text: txt } }); }; var payload = { text: 'Here are ' + news.length + ' new papers for *"' + keyword + '"* :eyes:', //failback sentence blocks: blocks }; // Post Slack on Incoming Hook var options = { method: "post", headers: {"Content-type": "application/json"}, payload: JSON.stringify(payload) }; UrlFetchApp.fetch(HookURL, options); // Record fetched items var guids = []; for each(var item in items) { guids.push(item.getChild('guid').getText()); }; properties.setProperty(keyword, guids.join(',')); }; }; };
NAACL 2019の医療関連論文を概観する.
North American Chapter of ACL (2019) - ACL Anthology
medic*, health, diseaseで検索.WS論文はおもしろそうなものだけ.
Biomedical Event Extraction based on Knowledge-driven Tree-LSTM - ACL Anthology
医学生物学分野におけるevent extractionにおいて背景を捉えるために外部知識を利用するknowledge base (KB) -driven tree-strucutred long short-term memory networks (Tree-LSTM)を提案.
Gene Ontologyにおけるentity typeとpropatyの記載からKB concept embeddingを作成し,sentence embeddingや他のword embeddingと組み合わせて使用した.説明的な文章の遠い依存関係をNNで捉えるために,先にe Stanford dependency
parserを用いて構文解析を行ったのちにtree-based LSTMを使用した.BioNLP2011のshared taskでstate-of-the-artを更新.
医療従事者によるアノテーションはハイコストだが,難しい文章のみを医療従事者に依頼すれば,効率的に有効なアノテーションができるのでは,という発想.crowdworkerのラベルのみで学習させたモデルと,そのラベルとの差を難しさとしてモデルを構築.このannotator間の不一致,とは相関していなかった.難易度の高い文章をコーパスから除くとむしろ学習結果が低下.その文章に医療従事者によるアノテーションを付加したところ学習結果が向上した.
→ weakly supervised learningとか,active learningにつながる話.医療コーパスはannotationがhigh costなのでこういう研究が出てくると有意義なコーパスづくりに繋がりそう.
Inferring Which Medical Treatments Work from Reports of Clinical Trials - ACL Anthology
毎日100以上のRCTが報告され,これを追うのは大変.Cochraneなど人手で情報収集している組織もあるが,NLPで自動化できる部分もあるのでは.本文から,介入,比較対象,アウトカムをアノテーションし,sig. decrease, no difference, sig increaseをラベル付けしたコーパスを作成した.annotation + RNNのモデルで推測.なお,データセットはgithubに公開されている.
→ 介入,比較対象,アウトカムを抜き出す部分こそ自動化したいところ.
A Survey on Biomedical Image Captioning - ACL Anthology
ワークショップ.レントゲン読影レポート自動生成についてのsurvey論文.2018年までに公開されたdatasetもまとめられている.
→ この論文のあと,2019年にかなり大規模なdatasetが相次いで公開されている.
Medical Entity Linking using Triplet Network - ACL Anthology
疾患表現からのentity linkingにおける候補疾患のランキング学習において,triplet networkを使用して学習したところ既存研究を上回る成績だった.
会話や言語機能にアルツハイマー型認知症の初期症状がでるというのはかねてから指摘されており,様々な言語で報告があるがいずれの研究でもsample数が少ないのが課題だった.言語間で共通するアルツハイマー型認知症初期の言語特徴を特定し,サイズの小さいフランス語データセットに比較的大きな英語データセットを加えることで,フランス語での識別能を向上させた.
dictationする部分と,文章からinformation unitを抽出する部分は人手.そこinformation unitのsequence上でLanguage Modelを構築しprobabilityなどを特徴量に使用.
→ 新規性がよくわからず....
東北大乾研から.Knowledge Graphは,(head, relation, tail)というtripletで表され,Relation Extraction, Question Answeringなど種々のNLPタスクで有用だが,医学用のKnowledge Graphは,FreeBaseやWikiDBなどの汎用Knowledge Graphに比べて成熟しておらず語彙数が不足している.コーパスからKnowledge Graphのためのrelationを自動的に抽出するシステムが望まれるが,こちらにも教師データが不足しているという問題がある.
RE modelとKnowledge Graph Completion (KGC) modelをjointly trainingするモデルが,汎用KGの構築に有用であり,こちらをbase modelとして,entity typeによる成約を加えたモデルでUMLS + Medlineコーパスで学習させたところ,十分に医学分野に適用可能であり,拡張も有効であった.
→ 文章からKnowledge Graphを構築できるのは強い.Medlineは公開用のかなり整った文が多いので学習がうまくいきやすく大規模Knowledge Graphの構築につながるのかもしれない.将来的にはこうやって自動生成されたKnowledge GraphがSNOMED CTにとって代わるのかも.NN構造はもう少し詳しく読んでみたい.